So this is a problem that was bugging me for some time now and I never found a chance to think about it thoroughly. The problem statement is simple: how to generate points within a circle in such a way that points’ distribution be uniform? One can assume that a rand() function is provided and that it returns a number between $0$ and $1$ with a uniform distribution. Once I investigated the problem in turned out being so fascinating I decided to write a blog post about it. Here it is.
For the sake of simplicity let’s assume that the our circle is a unit circle, i.e. a circle with radius of $1$.
The first solution that came into my mind was to generate an angle, between $0$ and $2\pi$, and a distance from the center between $0$ and $1$. Given specific angle $\alpha$ and distance $d$ we can generate a point using polar coordinates. To test this a created a small JavaScript program (code provided in the end) that generates $3000$ points within a circle. Here is what we get using the method above:
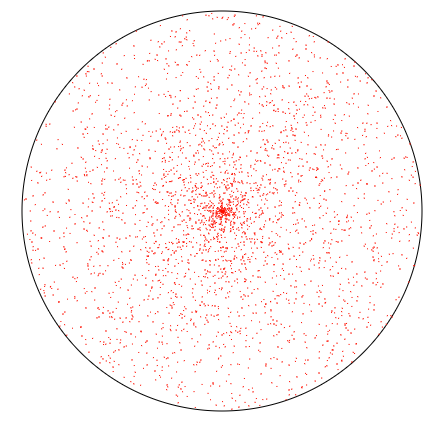
As you can see the distribution is far from uniform. There are much more points near the center than near the perimeter of the circle. Once you think about this, it is quite easy to explain why the distribution is indeed non uniform in this case. Let’s assume some angle $\alpha$ that was already chosen and now we need to generate the distance $d$. There is a $0.5$ probability for $d$ to be greater than $0.5$ and the same probability for it to be smaller. In other words there is a $0.5$ chance for the point to be within the circle with radius of $0.5$ and same chance for it to be outside of it. If you look at those two areas below it is clear that their areas differ. Therefore, given each has similar number of points, the distribution is not uniform.
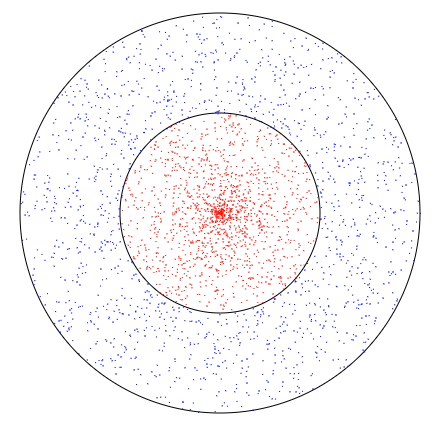
In fact, it would be good to show what is the exact difference between area sizes. The size of an area with blue dots equals . The size of an area with red dots equals . So we have similar number of points (which converges to being equal as the number of points approaches infinity) in two areas with one being $3$ times bigger than the other. A clear non uniform distribution.
So what is the right way?
We should start by noticing that there should be more probability to generate a point if the $d$ is bigger. To demonstrate this please see the image below. To have uniform distribution we need to to be able to generate more points for larger $d$ - blue points in the image below, and less points for smaller $d$ - red points in the image below.
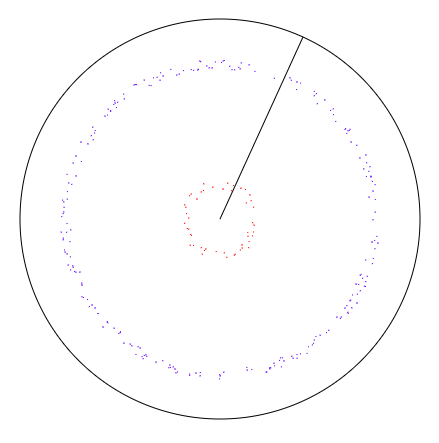
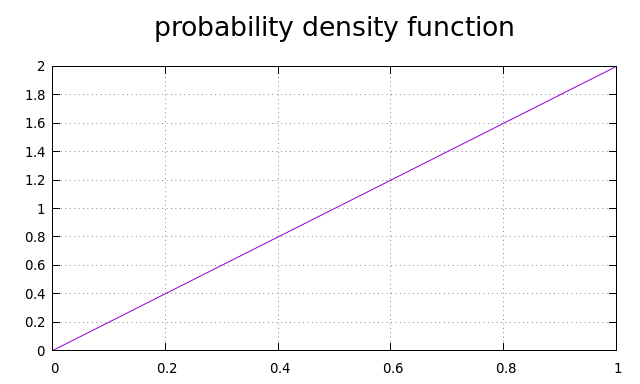
Given the above we notice that there is a correlation between the number of dots and the circumference of a circle with radius $d$. The larger the $d$, the larger the circumference, the more dots we need to be able to generate there to keep the distribution uniform. The length of the circumference of a circle given $d$ is $2\pi d$, so the relation between $d$ and circumference is linear. Thus the relation between $d$ and the number of dots with radius equal to $d$ is linear. Given this we can create a probability density function (PDF) for a range of $d$ between $0$ and $1$. We know that the x axis is defined to be between $0$ and $1$ (all possible radii). We know that for $d=0$ the probability should be $0$. We also know that the function is linear. Given that the area under PDF must equal $1$ we get the following:
Now we need a way to generate random numbers based on this PDF. How do we do it? Fortunately there is a method for this called inverse transform sampling. The method consists of the following $3$ steps:
- Create a cumulative distribution function (CDF) from PDF
- Find an inverse function to a CDF you have found in the previous step
- Generate uniformly distributed numbers and transform those through the inverse function from step $2$. The resulting numbers will have the probability distribution as the original PDF in step $1$
Let’s do it. Our PDF is . CDF is an integral of PDF. Therefore:
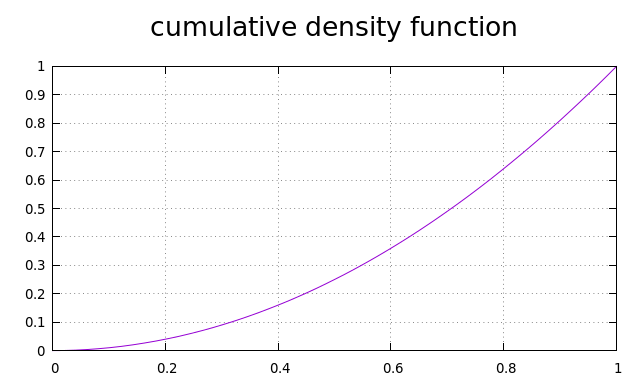
Now we need to find the inverse function for CDF(x). But it is clear. The inverse of a square is square root. So we get .
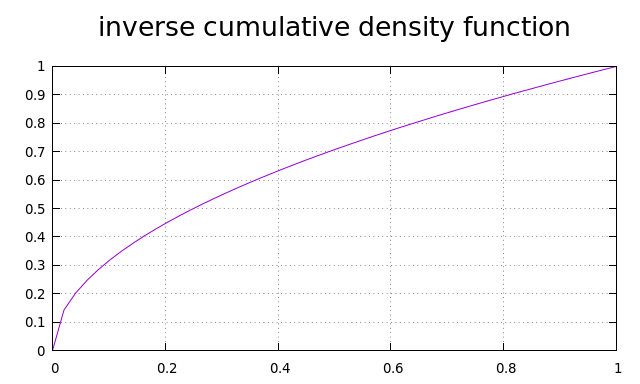
Now, if we generate numbers with uniform distribution, using rand(), and calculate a square root of each, we will get numbers that behave as we want. To recap, what we need to do now is to generate $\alpha$ as we did previously, then generate $d$ but before using $d$ apply a square root on it. If we do this we receive the following distribution. Exactly what we wanted.

Here is the code you can play with. It uses HTML’s canvas to drop the circle with 3000 uniformly generated points within. Just save the file as HTML and open it in you favorite browser (tested with Firefox and Chrome).
<!DOCTYPE html>
<html>
<body>
<canvas id="my_awesome_canvas" width="800" height="800"/>
</body>
</html>
<script type="text/javascript">
// Initialization of canvas and global vars
var c = document.getElementById("my_awesome_canvas");
var ctx = c.getContext("2d");
var center_x = 400;
var center_y = 400;
var radius = 200;
// Clear the canvas
ctx.clearRect(0, 0, center_x * 2, center_y * 2);
// Draw the circle
drawCircleCircumference();
// Generate and draw the dots
generateAndDrawPoints();
function generateAndDrawPoints() {
// Generate 3000 points
for (i = 0; i < 3000; i++ ) {
// Appying the sqrt() on the result of Math.random() is
// the most essential part here.
var random_rad = Math.sqrt(Math.random()) * radius;
var angle = Math.random() * 2 * Math.PI;
putPixelRad(angle, random_rad);
}
}
function drawCircleCircumference() {
ctx.beginPath();
ctx.arc(center_x, center_y, radius, 0, 2 * Math.PI);
ctx.stroke();
}
function putPixelRad(angle, radius) {
// Using simple transformation to linear coordinates
var x = center_x + radius*Math.cos(angle);
var y = center_y + radius*Math.sin(angle);
putPixel(x, y);
}
function putPixel(x, y) {
// It is better to use createImageData() here but
// it is not the essence of this code
ctx.fillStyle =
"rgba("+255+","+0+","+0+","+(255/255)+")";
ctx.fillRect( x, y, 1, 1 );
}
</script>
Thanks for reading!